强化学习问题的框架
强化学习教程-0, 杜新宇,京东, 2021
1.强化学习问题的框架
强化学习问题的常用框架是智能体-环境(agent-environment)模型,如下图[1]所示。
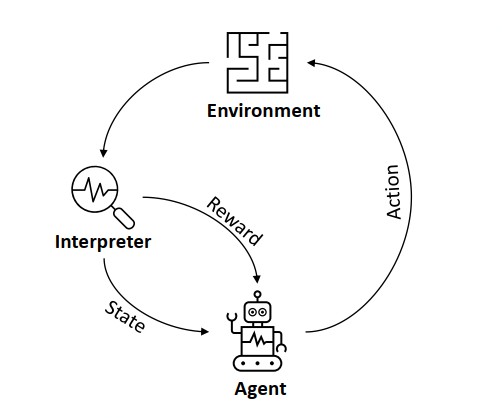
其中,agent负责学习和做决策,除agent以外的都称为environment,上图中的Environment和Interpreter其实都属于environment。在某个时刻t,agent通过观察环境的状态statet,做出决策,采取行动actiont,从环境获得收益rewardt+1并且通过观察得到一个新的状态statet+1。类比下棋可以很好的理解这个过程。
agent做决策的过程是典型的Markov decision process (MDP),可以用下述五元组的形式描述: \((\mathcal{S,A,R,P,\gamma})\)
其中\(\mathcal{S}\)为所有可能状态的集合,\(\mathcal{A}\)为所有可能行动或决策的集合,\(\mathcal{R}\)是收益函数,\(\mathcal{P}\)是状态转移概率,\(\mathcal{\gamma}\)是折扣因子,用来对远期收益进行折扣,即在计算收益时近期的收益占比重较大,越远期比重越小。
agent的目标就是学习一个策略\(\pi(a\vert s)\),使得在状态\(s\in\mathcal{S}\)的情况下采取行动\(a\in\mathcal{A}\),使得未来的累加收益总和的期望值最大化。
\[max \mathbb{E}[R(\mathcal{\tau})]\\ 其中,\mathcal{R(\tau)}=\sum_{t=0}^\tau\gamma^tr(a_t,s_t)\\ 0\le\gamma\le1\] 强化学习的主要目的是学习一个策略\(\pi(a\vert s)\), 使得累加收益期望最大化,该策略的数学形式为条件概率,即在状态s的情况下,采取动作a的概率。当算法在学习过程中采用相同的策略评价和改进时称为on-policy算法。如果产生数据的策略和被评估和改进的策略不相同,则该算法称为off-policy算法。
2.数学基础
2.1 期望值\(\mathbb{E}\)的定义为:
\[\mathbb{E}[f(x)] = \sum_xP(x)f(x)\\ 其中P(x)为变量x的概率函数,f(x)为自变量为x的函数。\]假如,x代表某单位员工的身高,f(x)为身高体重函数,P(x)为身高的概率函数,那么f(x)的期望值即为该单位员工的平均体重。
2.2 条件概率:
条件概率是指,在事件B发生的条件下,A事件发生的概率。条件概率表示为:
\[P(A\vert B)=\frac{P(AB)}{P(B)} \\ P(AB)为事件A和B同时发生的概率\\ P(B)为事件B发生的概率\]3.常用符号
| 符号 | 含义 |
|---|---|
| \(s\in\mathcal{S}\) | 状态 |
| \(a\in\mathcal{A}\) | 动作 |
| \(r\in\mathcal{R}\) | 收益 |
| \(S_t,A_t,R_t\) | 在一个迹内,时刻t的状态,动作和收益。有时也用小写字母。 |
| \(\gamma\) | 折扣系数,用来对未来收益进行折扣计算,该系数值在0到1之间。数学上采用折扣系数的作用是使得累加收益收敛到有限值。 |
| \(G_t\) | 累加收益;\(G_t=\sum_{k=0}^\infty\gamma^kR_{t+k+1}\) |
| \(P(s',r\mid s,a)\) | 状态转移概率,从状态\(s\)采取动作\(a\),获得收益\(r\),更新状态到\(s'\)的概率。 |
| \(\pi(a\mid s)\) | 概率形式得策略函数,在状态\(s\)下,采取动作\(a\)的概率。\(\pi_\theta(\cdot)\),表示用参数\(\theta\)拟合的策略函数。 |
| \(\mu(s)\) | 确定性策略函数,有时也用\(\pi(s)\)表示,表示在状态为\(s\)时的动作。 |
| \(V(s)\) | 状态价值函数,表示状态\(s\)下的期望累加收益。\(V_w(\cdot)\)表示用参数\(w\)拟合的状态价值函数。 |
| \(V^\pi(s)\) | 采用策略\(\pi\)处于状态\(s\)时,期望的累加收益。\(V^\pi(s)=\mathbb{E}[G_t\mid S_t=s]\) |
| \(Q(s,a)\) | 动作价值函数,表示状态\(s\)下采取动作\(a\)的期望累加收益。\(Q_w(\cdot)\)表示用参数\(w\)拟合的动作价值函数。 |
| \(Q^\pi(s,a)\) | 采用策略\(\pi\)的动作价值函数。\(Q^\pi(s,a)=\mathbb{E}_{a\sim\pi}[G_t\mid S_t=s, A_t=a]\) |
| \(A(s,a)\) | 优势函数,\(A(s,a)=Q(s,a)-V(s)\)。可以看做是动作价值函数的升级版,通过减去状态价值降低了动作价值的方差。 |
参考文献:
[1] https://arxiv.org/abs/2101.06286
