神经网络出现前的强化学习
强化学习教程-1, 杜新宇,京东, 2022
1.卖拐ENV
首先,我们根据小品卖拐的故事,构建一个超级简单的环境(ENV),该ENV可以根据action产生state和reward。这个ENV只有两个状态和两个动作,之所以称之为超级简单就是因为其动作空间和状态空间都很小。两个状态分别为:\(S_1\)相遇,\(S_2\)卖拐。两个动作分别为:\(A_1\)攀谈,\(A_2\)离开。上述ENV中,范伟就是agent。他可以根据不同的state,采取不同的action。在相遇这个状态时,范伟有两个选择,离开或者攀谈。如果选择攀谈这个动作,不会产生任何后果,ENV会给出reward=0,如果选择离开这个动作,大忽悠会说你看他腿有病,给范伟心灵造成小伤害但是没有被骗,ENV会给出reward=10。在卖拐这个状态时,范伟也有两个选择,攀谈和离开。如果继续攀谈就会被忽悠住,因此ENV给出reward=-100。如果离开,则没被忽悠住,ENV给出reward=100。
2.基本概念
\[\begin{array}{l} Reward \quad R_t, \quad agent给出动作A_{t-1}后,ENV返回给agent的奖励或收益。\\如上ENV中,在相遇这个状态(S_1)范伟给出动作离开(A_2)获得的奖励为R_2=10. \end{array}\] \[\begin{array}{l} Return \quad G_t=\sum_{k=0}^\infty\gamma^kR_{t+k+1}, \quad 从t时刻到结束状态累加的奖励。\\\gamma\in(0,1)为累加因子,离当前时间越远的奖励,占比越小。\\比如在状态相遇时范伟采取攀谈这个动作,在状态卖拐时,范伟采取离开这个动作,\\那么G_1=\gamma*R_2+\gamma^2*R_3=\gamma*0+\gamma^2*100=100\gamma^2 \end{array}\] \[\begin{array}{l} State\quad Value \quad V(S_t)=\mathbb{E}[G_t|S_t=s]=\mathbb{E}[\sum_{k=0}^\infty\gamma^kR_{t+k+1}|S_t=s],\\状态s的价值函数,用累加收益的期望来刻画。\\如上所示,在状态S_t的累加收益G_t存在多种取值,比如在状态相遇时范伟采取攀谈\\这个动作,但在状态卖拐时,范伟不采取离开这个动作而是继续攀谈。\\那么G_1=\gamma*0+\gamma^2*(-100)=-100\gamma^2\\因此,需要用累加收益的期望值来刻画状态价值V(s) \end{array}\] \[\begin{array}{l} State-Action\quad Value\quad Q(S_t,A_t)=\mathbb{E}[\sum_{k=0}^\infty\gamma^kR_{t+k+1}|S_t=s,A_t=a]\\和状态价值函数类似,状态-动作价值函数也可以用累加收益的期望来刻画。\\只不过这个收益是在状态s采取具体动作a时产生的。 \end{array}\]有了\(Q(S_t,A_t)\)的定义,我们就可以构建一个Q表格。表格的行数为状态数,列数为动作个数。以我们卖拐ENV为例,可以绘制如下2x2的表格。该表格就是老范行动的指导方针,或称为策略。在相遇状态,老范就可以参看该表的第一行,看看那个动作对应的Q值大,选择Q值大的那个动作执行。以此类推,完成整个和ENV的交互过程。
 \(A_1\)=攀谈 \(A_1\)=攀谈 |  \(A_2\)=离开 \(A_2\)=离开 | |
|---|---|---|
 \(S_1\)=相遇 \(S_1\)=相遇 | \(Q(S_1,A_1)\) | \(Q(S_1,A_2)\) |
 \(S_2\)=卖拐 \(S_2\)=卖拐 | \(Q(S_2,A_1)\) | \(Q(S_2,A_2)\) |
3.算法
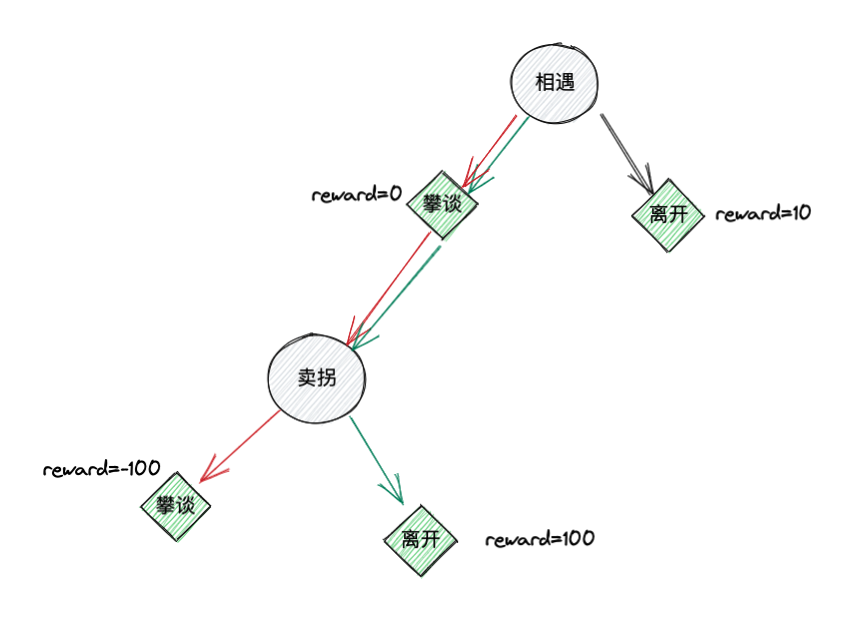
上图中每个灰色圆形代表一个状态,每个绿色菱形代表一个动作,动作边上标注了该动作获得的reward。该图是对ENV的一个可视化描述。从图中可以看出,按照绿色箭头的方向和ENV交互可以获得最大的累加收益,按红色箭头的方向获得的累加收益最小(这里假设累加因子\(\gamma=1\))。从交互开始到交互结束,称为一个episode,可以类比为游戏里面的一局。每采取一个动作后,ENV返回一个新状态并给出reward,称为一个step,可以类比为游戏里面的一个回合。从上图可以看出,黑色箭头所代表的episode只有一个step就结束了,而红色和绿色箭头所表示的episode有两个step。
当范伟遇见大忽悠时,他并不知道ENV根据他的各种action会反馈多少reward,这对他来说是未知的。这就需要他和ENV持续不断的交互,来获得ENV的信息,从而获得上述Q表格中的具体值。这个过程就是训练。
3.1时序差分(TD, Temporal-Difference Learning)
\(\begin{array}{l} V(S_t)\leftarrow V(S_t)+\alpha[G_t-V(S_t)] \end{array}\)
上式为TD算法的核心,\(\alpha\)为学习率。其余各项定义在基本概念中已给出。上式的意义为:在agent与ENV交互的过程中,每次agent处于状态\(S_t\),都需要更新状态价值。更新方法是将累加收益与状态价值的差乘以学习率当做更新值,加到之前的状态价值上。当进行了许多次更新后,状态价值与累加收益的差将变得非常小,状态价值最终收敛到累加收益处。将上式右侧做一下展开推导:
\(\begin{array}{l} \quad V(S_t)+\alpha [G_t-V(S_t)]\\ =V(S_t)+\alpha[\sum_{k=0}^\infty\gamma^kR_{t+k+1}-V(S_t)]\\ =V(S_t)+\alpha[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)-V(S_t)]\\ =V(S_t)+\alpha [R_{t+1}+\gamma G_{t+1}-V(S_t)]\\ \approx V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)]) \end{array}\)
上述推导最后一步用状态价值替代了累加收益,也是基于随着训练的进行,状态价值将收敛到累加收益。因此,TD算法更新状态价值的公式为:
\(V(S_t)\leftarrow V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)]\)
但是,知道状态价值并不能指导agent做出聪明的行动。比如在相遇这个状态,即使范伟知道了这个状态价值的确定值,也不能决定怎么做更好。而能够做出行动指导的是状态-动作价值,也就是Q表格中的值。Q相对于V来说多了一个限制条件-动作。例如,处于相遇状态时,Q给出采取攀谈这个动作的价值为30,采取离开这个动作的价值是20。那么范伟就完全可以做出聪明的动作了。Q的定义在基本概念已给出,类比上述推导过程可得更新Q的公式为:
\(Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)]\)
观察上式可知,更新一次Q需要\(S_t,A_t,S_{t+1},A_{t+1}\)这个四个量,因此,该算法也称为Sarsa(State-Action-Reward-State-Action)。
算法描述如下:
- 初始化Q表格,表格行数为状态集合中的元素个数,表格列数为动作集合中的元素个数。我们卖拐例子的Q表格是2x2的。Q表格中的值初始化为全0。
- agent处在任何状态\(S_t\)下,采取的动作\(A_t\)通过查Q表确定。采取的动作为该行Q值最大对应的动作。
- agent采取动作后ENV给出reward \(R_{t+1}\)和下一个状态\(S_{t+1}\)。
- 根据Q表格选择状态\(S_{t+1}\)下的最佳动作\(A_{t+1}\)。
- 更新Q:
如果\(S_{t+1}=terminal\),即episode结束,更新Q:
\(Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}-Q(S_t,A_t)]\)
否则,更新Q:
\(Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)]\)
回到第3步。
3.2 Q-Learning
Sarsa算法的第2步和第4步选取动作时,使用的Q表格为同一个。因此,该算法属于On-Policy算法。也就是选取\(A_t和A_{t+1}\)时,遵循的是同一个策略。我们也可以在一个回合结束后就更新Q表格,然后用更新后的Q表格确定\(A_{t+1}\)。走一步更新一次,这样更符合直觉。要达到这个效果,原理上需要将Sarsa算法中\(A_{t+1}\)这项去掉。
\(\begin{array}{l} \quad A_{t+1}=\arg\max \limits_a Q(S_{t+1},a)\\ 将上式带入\\ \quad Q(S_{t+1},A_{t+1})\\ =Q[S_{t+1},\arg\max\limits_a Q(S_{t+1},a)]\\ =\max \limits_{a \in A} Q(S_{t+1},a) \end{array}\)
上式加了max使得\(A_{t+1}\)消失。将上式带入Sarsa的更新公式得:
\(\begin{array}{l} Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma \max \limits_{a \in A} Q(S_{t+1},a)-Q(S_t,A_t)] \end{array}\)
因此算法描述如下:
- 初始化Q表格,表格行数为状态集合中的元素个数,表格列数为动作集合中的元素个数。我们卖拐例子的Q表格是2x2的。Q表格中的值初始化为全0。
- agent处在任何状态\(S_t\)下,采取的动作\(A_t\)通过查Q表确定。采取的动作为该行Q值最大对应的动作。
- agent采取动作后ENV给出reward \(R_{t+1}\)和下一个状态\(S_{t+1}\)。
- 更新Q:
如果\(S_{t+1}=terminal\),即episode结束,更新Q:
\(Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}-Q(S_t,A_t)]\)
否则,更新Q:
\(Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma \max \limits_{a \in A} Q(S_{t+1},a)-Q(S_t,A_t)]\)
回到第2步。
可以看到,Q-learning算法每执行一个回合就更新一次Q表格。只需要从ENV获得下一个状态就可以更新Q表格。两次action遵循的是不同的策略,因此属于off-policy算法。
3.3 冒险
上述算法不论Sarsa还是Q-learning,都存在一个bug。即由于\(\arg\max\limits_a Q(S_{t+1},a)\)的存在,使得在agent与ENV交互时总是走老路(比如卖拐例子中,总是走图中黑色箭头的路径),尤其当你用0初始化Q表格时。这样无论训练多少个episode,都不可能得到最优解。我们采取的办法是让agent有一定概率\(\epsilon\)不按照\(\arg\max\limits_a Q(S_{t+1},a)\)这种贪婪的策略采取行动,而是随机选一个动作执行。因此,\(1-\epsilon\)概率用贪婪策略选动作执行,\(\epsilon\)概率随机选动作执行。称这种策略为\(\epsilon-greedy\)策略。将这种冒险策略加到上述的算法中去,就形成了完整的Sarsa和Q-learning算法。
4. 是时候展现真正的技术了
上代码:
首先,根据我们卖拐的剧情,构建一个简单的ENV类。ENV类只包括两个方法,reset和step。reset负责重置ENV,step负责和agent交互。
import numpy as np
class ENV(object):
def __init__(self):
self.terminal = False
self.state = 0 #0代表状态相遇,1代表状态卖拐。
def reset(self):
self.terminal = False
self.state = 0
return self.state
def step(self, action):
'''根据action返回reward和新的state
action为0代表攀谈,1代表离开。
'''
if self.state == 0: #相遇
if action==0: #攀谈
self.reward = 0
self.state = 1
else: #离开
self.reward = 10
self.terminal = True
else: #卖拐
if action==0: #攀谈
self.reward = -100
self.terminal = True
else: #离开
self.reward = 100
self.terminal = True
return self.state, self.reward, self.terminal
然后,我们构建Agent类。SarsaAgent和QLAgent分别代表Sarsa和Q-learning两种算法。
class SarsaAgent(object):
def __init__(self, state_dim, action_dim, learning_rate=0.1, gamma=0.9, epsilon=0.1):
self.state_dim = state_dim #状态空间大小,有多少个状态就是几。
self.action_dim = action_dim #动作空间大小,有多少个动作就是几。
self.alpha = learning_rate #学习率,对应公式里的alpha
self.gamma = gamma #累加因子对应公式里的gamma
self.epsilon = epsilon #冒险系数,对应公式里的epsilon
self.Q = np.zeros([state_dim, action_dim]) #Q表格,有多少个状态就有多少行,有多少个动作就有多少列。
def getAction(self, current_state):
random_p = np.random.uniform(0,1) #在标准高斯分布上随机选一个值
if random_p<(1-self.epsilon): #如果随机值小于1-epsilon,则根据Q表格查询在当前状态下的最优动作。
action = self.getActionByQ(current_state)
else: #否则,随机选取一个动作。
action = np.random.choice(self.action_dim)
return action
def getActionByQ(self, current_state):
'''
根据状态,查Q表格获得最优action
'''
Q_row = self.Q[current_state] #从Q表格中选出目前状态对应的行。
maxQ = np.max(Q_row) #获得改行的最大值。
actions = np.where(Q_row==maxQ)[0] #将所有最大值所对应的列号组成动作集合。
action = np.random.choice(actions) #在动作集合中随机选取一个动作。
return action
def learn(self, current_state, action, reward, next_state, next_action, terminal):
'''
Q(S_t,A_t) <- Q(S_t,A_t) + alph[R_t+1+gamma*Q(S_t+1,A_t+1)-Q(S_t,A_t)]
根据算法中的更新公式,更新Q表格中当前状态(行),当前action(列)的对应值Q_sa
'''
Q_sa = self.Q[current_state][action] #当前Q值
Q_sa_next = self.Q[next_state][next_action] #下一时刻Q值
if terminal: #episode结束时,更新Q值
self.Q[current_state][action] = Q_sa + self.alpha*(reward-Q_sa)
else: #更新Q值
self.Q[current_state][action] = Q_sa + self.alpha*(reward + self.gamma*Q_sa_next-Q_sa)
def showQTable(self):
print(self.Q)
class QLAgent(SarsaAgent):
def learn(self, current_state, action, reward, next_state, next_action, terminal):
'''
Q(S_t,A_t) <- Q(S_t,A_t) + alph[R_t+1+gamma*maxQ(S_t+1,a)-Q(S_t,A_t)]
根据算法中的更新公式,更新Q表格中,当前状态(行),当前action(列)的对应值Q_sa
'''
Q_sa = self.Q[current_state][action] #当前Q值
Q_s_next = self.Q[next_state] #下一状态Q值
if terminal: #episode结束时,更新Q值
self.Q[current_state][action] = Q_sa + self.alpha*(reward-Q_sa)
else: #更新Q值
self.Q[current_state][action] = Q_sa + self.alpha*(reward + self.gamma*np.max(Q_s_next)-Q_sa)
最后,我们让Agent和ENV多次交互从而达到训练目的。
def episode(env, LF):
'''
agent与ENV互动一个episode,
在此过程中对Q表格进行更新,直到episode结束。
env: ENV对象
LF: 老范的拼音缩写, Agent的对象
'''
total_reward = 0 #一个episode获得的总reward
state = env.reset() #初始化ENV
action = LF.getAction(state) #根据state获得action
while True:
next_state, reward, terminal = env.step(action) #用action跟ENV互动,获得下一个状态,reward和是否episode结束标志符
next_action = LF.getAction(next_state) #根据下一个state获得下一个action
LF.learn(state,action,reward,next_state,next_action,terminal) #更新Q表格
total_reward += reward #累加reward
action = next_action #准备下一次互动,更新action
state = next_state #准备下一次互动,更新state
if terminal: #到达终点则结束循环
break
return total_reward
env = ENV()
###以下算法二选一,注释掉不用的那行###
LF = SarsaAgent(2,2) #这里让老范具有sarsa算法的思维
# LF = QLAgent(2,2) #这里让老范具有Q-learning散发的思维
LF.showQTable()
for ep in range(1, 200):
total_reward = episode(env, LF)
if ep%10==0:
print("Episode {}, Total reward {}".format(ep, total_reward))
LF.showQTable()
运行上述代码的输出如下所示(由于代码中存在随机采样,因此你运行的结果与我的不可能完全相同):
[[0. 0.]
[0. 0.]]
Episode 10, Total reward 10
[[0. 6.5132156]
[0. 0. ]]
Episode 20, Total reward 10
[[0. 8.78423345]
[0. 0. ]]
Episode 30, Total reward 10
[[0. 9.57608842]
[0. 0. ]]
Episode 40, Total reward 10
[[0. 9.85219117]
[0. 0. ]]
Episode 50, Total reward 10
[[0. 9.94846225]
[0. 0. ]]
Episode 60, Total reward 10
[[0. 9.9820299]
[0. 0. ]]
Episode 70, Total reward 10
[[ 0. 9.99226446]
[-10. 10. ]]
Episode 80, Total reward 10
[[ 0.9 9.99700309]
[-10. 19. ]]
Episode 90, Total reward 10
[[ 0.9 9.99895504]
[-10. 19. ]]
Episode 100, Total reward 10
[[ 0.9 9.99963565]
[-10. 19. ]]
Episode 110, Total reward 10
[[ 0.9 9.99987296]
[-10. 19. ]]
Episode 120, Total reward 10
[[ 2.52 9.99995078]
[-10. 27.1 ]]
Episode 130, Total reward 10
[[ 2.52 9.99998284]
[-10. 27.1 ]]
Episode 140, Total reward 10
[[ 2.52 9.99999402]
[-10. 27.1 ]]
Episode 150, Total reward 10
[[ 2.52 9.99999791]
[-10. 27.1 ]]
Episode 160, Total reward 10
[[ 2.52 9.99999927]
[-10. 27.1 ]]
Episode 170, Total reward 100
[[ 13.472496 9.99999961]
[-10. 52.17031 ]]
Episode 180, Total reward 100
[[ 43.67449528 9.99999965]
[-10. 81.46979811]]
Episode 190, Total reward 100
[[ 61.82752158 9.99999965]
[-19. 92.82102012]]
从运行结果可以看出,初始Q表格都是0。当训练了170个episode后,老范具有了真正的智慧。他可以在交互过程中采取更聪明的action,获得最大的累加收益。从运行结果能看出强化学习的几个特点:1.需要Agent和ENV不断交互进行训练。2.强化学习不止考虑当前利益,而是通过考虑长远利益而采取行动。比如,在相遇状态时,离开reward=10,而攀谈reward=0,如果只考虑当前利益的话一定会选择离开。而强化学习算法引入了冒险、累加收益等机制。通过多次互动,全面的学习ENV内在运行机制,从而选择最佳action获得全局最大收益。3.强化学习擅长决策问题,通过构建一个策略(Q表格),来选择更聪明的action,从而获得全局最大收益。
最后对比理解一下Sarsa和Q-Learning算法的差异。从代码可以看出,SarsaAgent是QLAgent的基类。两种算法除了learn方法不同,其余完全一致。在learn方法中,不同处仅仅为方法内最后一行更新Q值的代码。
#Sarsa算法如下:
self.Q[current_state][action] = Q_sa + self.alpha*(reward + self.gamma*Q_sa_next-Q_sa)
#Q-Learning算法如下:
self.Q[current_state][action] = Q_sa + self.alpha*(reward + self.gamma*np.max(Q_s_next)-Q_sa)
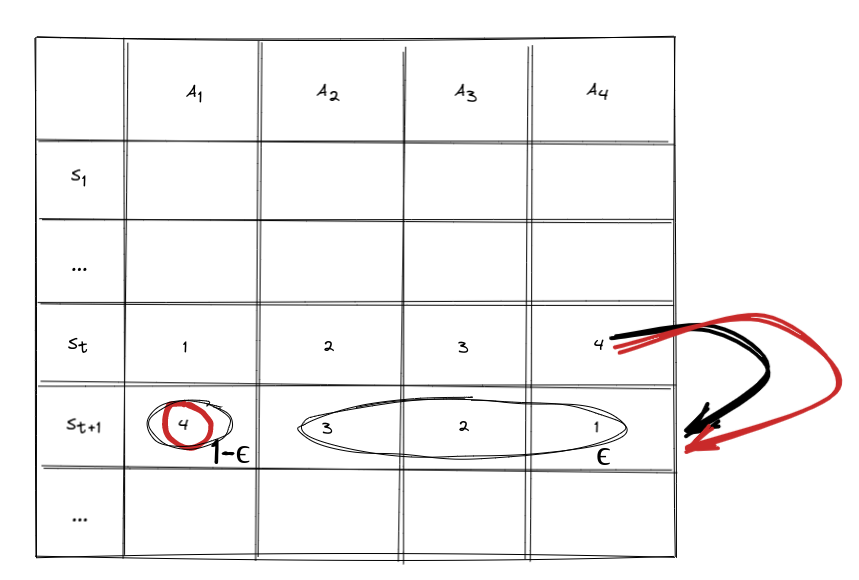
可以看出,不同处为等号右侧括号内第二项乘号右侧项,称之为更新项。Sarsa为Q_sa_next,即根据下一个状态,下一个动作查表得到的Q值。Q-Learning为np.max(Q_s_next),即下一个状态中,最大的Q值。如下图红色标注所示,Q-Learning算法中,更新项为确定的。从状态\(S_t\)转移到状态\(S_{t+1}\)的过程中,该项为红色圆圈标注的该行最大值。而Sarsa算法中,更新项不确定,因为在状态转移过程中,Sarsa算法需要先确定\(A_{t+1}\),在这个过程中由于冒险机制的存在,有一定概率挑选的Q值不是该行最大的,如图中黑色标注所示。上述差异使得Q-Learning算法比Sarsa算法更激进些,收敛相对较快。