神经网络出现后的强化学习(深度强化学习)-DQN(deep Q-network)算法
强化学习教程-2, 杜新宇,京东, 2022
1.神经网络
1.1 网络结构
神经网络就是由输入层,隐藏层和输出层构成,如下图所示。一个神经网络只有一个输入层和一个输出层,可以有多个隐藏层。圆圈内的符号\(b_j^l\)是偏移量,上角标为所处的层数,下角标为位于本层从上到下数第几个。连线上的符号\(w_{jk}^l\)是权重,上角标表示箭头指向的神经元所处的层数,下角标第一个数字代表箭头指向的神经元所处的位置,第二个数字代表发起箭头的神经元所处的位置。输出箭头上的符号\(a_j^l\)表示第l层,第j个神经元的激活函数。
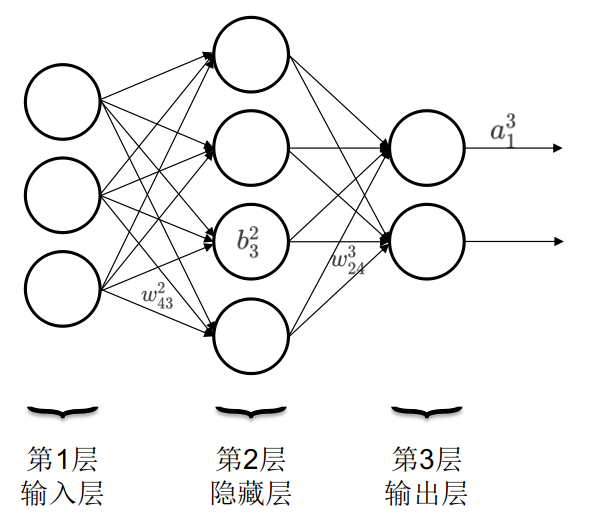
1.2 训练机制
当我们构建了一个神经网络后,其最初的权重\(w_k\)和偏移量\(b_l\)都是随机的。这种神经网络并不能正确执行任务。我们还需要对其进行训练,使其在给定输入数据\(x\)时的输出\(o\)与\(x\)的标注值\(L(x)\)尽量相近,这种用于训练神经网络的数据集称为训练数据集。我们希望\(L(x)和o\)这两个向量之差的几何距离\(\parallel L(x)-o\parallel\)越短越好,该函数称为Loss function。几何距离越短神经网络的实际输出和我们期望的输出越相近。而且我们希望神经网络在训练数据集的所有训练数据上都实现短的几何距离,即要求\(\sum_{i=1}^n \parallel L(x)-o\parallel\)尽量小,该函数称为Cost function。我们可以通过梯度下降及其衍生方法,来调整网络中的参数(权重和偏移量),使得Cost function达到最小值。该过程就称作神经网络的训练过程。
2.用神经网络替换Q表格
上一节,介绍TD和Q-Learning算法时,用了一个简单的例子-卖拐。在卖拐的ENV中,状态是离散值,要么是0代表相遇,要么是1代表卖拐。这种场景可以很好的用TD或Q-Learning算法解决。因为状态值离散且有限,意味着Q表格的行数是一定的。而在有些场景下,状态是连续的,即使强行使其离散化,也会导致状态数目太多,由于内存无法存储超多行数的Q表格而无法计算。因此,我们需要找到一种方法,该方法可以接收连续状态值,输出该状态下不同action的Q值。这时,神经网络就走上了舞台中央。在强化学习中,神经网络(NN-Neural Network)的作用是拟合Q值。通过agent和ENV的多次互动来获得训练NN的数据。
在Q-Learning算法中,更新Q值的公式为:
\(\begin{array}{l} Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma \max \limits_{a \in A} Q(S_{t+1},a)-Q(S_t,A_t)] \\ TargetQ = R_{t+1}+\gamma \max \limits_{a \in A} Q(S_{t+1},a) \end{array}\)
我们将上式中括号内,减号左边的项称为TargetQ值。在Q-Learning算法中,就是让Q值去不断的逼近TargetQ值。一旦Q=TargetQ,上式中括号内为0,Q值不再更新,训练也就完成了。当然这是理想情况,一般不会发生。
因此,我们可以构建NN的Loss function为:
\(\begin{array}{l} LOSS_{DQN}=\parallel Target Q-Q \parallel \\ \quad \quad \quad\quad\quad=[R_{t+1}+\gamma \max \limits_{a \in A} Q(S_{t+1},a)-Q(S_t,A_t)]^2 \end{array}\)
因此,我们只需要用梯度下降等方法,根据Loss function来优化NN的参数即可。至此,我们找到了用神经网络代替Q表格,来进行强化学习的方法。这种将多层神经网络和强化学习相结合的方法称为深度强化学习DRL。
